Stack ist ein Fragetyp für Moodle, der besonders geeignet ist für Mathematik. Er bietet eine CAS-Unterstützung an, die ermöglicht, auch folgerichtige Antworten automatisch zu beantworten. Diese Woche habe ich mich mit meiner Lieblingskollegin hingesetzt, die Grundlagen dieses Fragetypen zu lernen.
Hier sind einige Lernquellen: TU-Clausthal, TU Stuttgart.
- Das Anlegen der Fragen erfolgt wie gewohnt. Im Fragetext werden Input- und Validierungsvariablen definiert, die später als Eingabefelder erscheinen. Da drum kann man normal mit Latex und dem Texteditor arbeiten.
- Die zugrundeliegende Sprache bzw. CAS ist Maxima und man ruft Maxima-Code im normalen Text, auch in Latex-Umgebungen, mit {@ Maximainhalt @} auf.
- Es können beliebig viele Input-Felder definiert werden. Wir haben erstmal zwei Felder genutzt.
- Der Voreintrag bei „spezifisches Feedback“ darf nicht gelöscht werden.

Das war unsere erste Aufgabenstellung. Vertieft haben wir uns dann in zwei Bereiche: Den Termbaum, der die Struktur des Terms in der allgemeinen Rückmeldung zeigt und die Nutzung von Variablen.
Der Termbaum mit HTML
Es gibt einen Maxima-Befehl (disptree), der eine Baumstruktur eines Termes in HTML automatisch erzeugt. Der sieht allerdings nicht gut aus, weil die Werte von Latex-Klammern umgeben sind und für die fünfte Klasse passt auch / als Geteilt-Zeichen nicht. Man kann den Befehl wie folgt verbessern:
Variablen und Rückmeldebäume
Variablen werden global für die gesamte Frage im Feld „Aufgabenvariablen“ definiert und wir haben uns an den Tipp gehalten, Variablen auch für die korrekten Lösungen einzuführen. Dann muss man später nur oben etwas ändern und alle Überprüfungen usw. passen sich automatisch an. Hier ist unser Variablenfeld:

Wir haben hier schon Zufallszahlen benutzt. Da beim zweiten Summanden und dem Divisor ab und zu mal eine Null herauskam, haben wir uns dazu entschieden, dass diese Zahlen aus einer festen Liste zufällig gewählt werden sollen. Der Dividend, der später in der Aufgabe auch zu sehen sein soll, wird dann berechnet. Ein wenig Schwierigkeiten hat uns dabei die Einstellung zum automatischen Vereinfachen gemacht. Unter „Optionen“ gibt es „Aufgabenweites Simplify“. Wenn man das ausmacht – weil man zum Beispiel bei der Rückmeldung ja einzelne Schritte prüfen will und daher keine Vereinfachung der Terme möchte – dann wird auch die Rechnung oben nicht mehr vereinfacht.
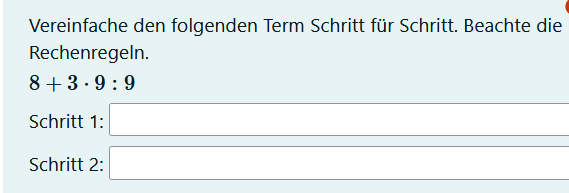
Das war nicht so ganz, was wir uns gedacht hatten, eigentlich sollte dort statt 3 mal 9 18 stehen, so dass die Schüler* selbst die Rechnung ausführen müssen. Wenn man Simplify aufgabenweit anschaltet, werden aber die Terme der Musterlösungen auch vereinfacht, was vielleicht nicht Sinn der Sache ist. Man kann das umgehen, indem im Textfeld des Aufgabentextes statt {@Divident@} schreibt: {@ev(Dividend,simp)@} – dann wird der Ausdruck dort und nur dort vereinfacht.
Update:
Nun habe ich mal eine Boolean-Variable, also den Fragetyp True/False ausprobiert. Man definiert einfach die Variable „loes1“ mittels „loes1:true;“ und stellt den Antworttyp nach dem ersten Speichern passend ein. Dann kann man wie gewohnt ans1 gegen loes1 mit string oder algequiv prüfen. Man könnte auch bei TAns die Antwort „true“ eingeben, aber ich finde es besser, die Lösung oben mit zu sehen und beim Duplizieren schnell umstellen zu können.
